Neues IDE-Interface von dbox2.com

[kpt.ahab]

ohhh bist du gut, frage mich nur warum du nicht selber eine Platine baust.
Und zeigst uns allen mal wie du das machen würdest.!

Schade, dass auch deine Reaktion auf Verbesserungen so negativ ausfällt.
Ich hatte wirklich den Glauben, dass auch du deutlich mehr Sachverstand aufweist und nicht so hochnäsig reagierst wie gurgel oder Gorcon.

Ja klar habe ich immer ein offenes Ohr für Verbesserungen, aber wie bitsucker mit dem Text rüber gekommen ist, war auch nicht so tolle.

Hätte er mal geschrieben...

>@käppi
>habe da einen vorschlag eine Verbesserung bla bla bla .. u.s.w

Dann hätte man sich auch besser unterhalten können, das mit dem Eingangskondensator ist ja auch richtig, der kommt noch druf.

Na ja mal sehen was die Leute wieder auszusetzen haben, wenn ich die erste Platine mit FPGA und (?DMA?) hier poste..... bin gerade am Layout dran.

[PT-1]

@kpt.ahab

Geschrieben ist immer schnell etwas ... Nur ob man es dann auch 100% so meint wie der jenige der es liest ist manchmal nicht der Fall.

Gruss

PT-1

[eule]

Ob der Wirkungsgrad hier nun tatsächlich so viel schlechter ist, dass sich das spürbar bei der Stromaufnahme bemerkbar macht würde ich jetzt so nicht unterschreiben. Das müsste man erst mal messen. Über 77% kommt der Regler hier aber sowieso nicht.

Das mit den 77% hast du bestimmt aus dem Datenblatt? Die gelten nur bei einer Belastung des Ausgangs mit 3A.

Bei optimaler Auslegung der Bauteile und Belastung mit nur 500mA kann der Wirkungsgrad bis 90% gehen.

ne Begründung für die Verwendung eines 100nf statt 100µF hätte doch gereicht

Ich vermute mal, dass ein 100nF Kondensator ausreicht, da die Eingangsspannung ja schon gesiebt ist. Damit müssen nur kleine Spannungsabfälle durch den ohmschen Widerstand der Zuleitung abgefangen werden um einen stabilen Betrieb des Schaltkreises zu gewährleisten. Diese Lösung ist für mich jedenfalls vollkommen in Ordnung, sofern der Kondensator sehr nahe am Schaltkreis plaziert wurde.

[Gorcon]

Eigentlich gehört immer beides drauf ein 100nF Kondensator so dicht wie möglich am Chip und zusätzlich ein Elko.

Gruß Gorcon

[bitsucker]

Das mit den 77% hast du bestimmt aus dem Datenblatt? Die gelten nur bei einer Belastung des Ausgangs mit 3A.

Bei optimaler Auslegung der Bauteile und Belastung mit nur 500mA kann der Wirkungsgrad bis 90% gehen.

Hmm, da interpretiere ich das Datenblatt anders. Der maximale Wirkungsgrad von 88% geht da von Volllast (3A) und 12V Ausgangsspannung aus. Bei geringerer Belastung bzw. geringerer Ausgangsspannung geht der Wirkungsgrad runter.

In dem National Datenblatt sieht man das besser, da ist ein entspr. Diagramm drin. Der max. Wirkungsgrad von unter 90% wird da bei 15V Ausgangsspannung und 3A Last erreicht. Bei 5V ist der Wirkungsgrad deutlich geringer.

Ich vermute mal, dass ein 100nF Kondensator ausreicht, da die Eingangsspannung ja schon gesiebt ist.

Der Sinn des Eingangskondensators ist allerdings nicht, die Qualität der Versorgungsspannung zu verbessern (die sollte bereits i.O. sein), sondern eine gleichmässigere Stromaufnahme und damit letztlich geringere Störstrahlung zu erreichen und dafür reichen die 100nF nicht.

@gorcon

Schaden wird der 100nF hier sicherlich nicht, aber ich denke auch nicht, dass er irgendwas bringt. Ist so auch nirgendwo in den Applikationsbeispielen zu finden.

[Gorcon]

Schaden wird der 100nF hier sicherlich nicht, aber ich denke auch nicht, dass er irgendwas bringt. Ist so auch nirgendwo in den Applikationsbeispielen zu finden.

Nein, schaden tut er auch nicht, aber in meinen Aplikationen war er vorgegeben (ebenso der Elko).
Auf meinen Platinen habe ich den daher auch drauf. Das Layout entspricht weitgehenst der Vorgabe.

Gruß Gorcon

[eule]

Hmm, da interpretiere ich das Datenblatt anders. Der maximale Wirkungsgrad von 88% geht da von Volllast (3A) und 12V Ausgangsspannung aus. Bei geringerer Belastung bzw. geringerer Ausgangsspannung geht der Wirkungsgrad runter.

Wie kann man ein Datenblatt aber auch sooo fehlinterpretieren....
Wäre in dem Datenblatt ein Diagramm Wirkungsgrad in Abhängigkeit vom Laststrom (nicht Spannung), hättest du den Müll nicht geschrieben.

Der Wirkungsgrad steigt, je geringer die Belastung des Ausgangs ist und wird nur durch den Eigenverbrauch des Schaltkreises begrenzt. Weiterhin hängt der Wirkungsgrad von der verwendeten Diode ab. Je höher die Durchlasspannun ist, desto geringer ist der Wirkungsgrad. Da bei allen Dioden die Durchlasspannung steigt, wenn der Durchlasstrom erhöht wird, fällt auc der Wirkungsgrad. Wenn man die Schaltung für max. 1,5A Dauerbelastung auslegt, kann man auf Dioden zurückgreifen, die eine deutlich geringere Durchlasspannung aufweisen als Dioden für 3A.

In dem National Datenblatt sieht man das besser, da ist ein entspr. Diagramm drin. Der max. Wirkungsgrad von unter 90% wird da bei 15V Ausgangsspannung und 3A Last erreicht. Bei 5V ist der Wirkungsgrad deutlich geringer.

Schade, dass in der Applikationsschrift nicht ein ähnliches Diagramm wie Dieses enthalten ist:

Der Sinn des Eingangskondensators ist allerdings nicht, die Qualität der Versorgungsspannung zu verbessern (die sollte bereits i.O. sein), sondern eine gleichmässigere Stromaufnahme und damit letztlich geringere Störstrahlung zu erreichen und dafür reichen die 100nF nicht.

Wenn du schon die Applikationsschrift zitierst, warum erwähnst du nicht, dass auch 100µF nicht ausreichen?

Um Störstrahlung vom Eingang des Schaltkreises zu unterdrücken ist ein 100nF Kondensator weit besser geeignet als ein 100µF Elko mit seinen langen Anschlußdrähten und dicken Wicklungen (ohmsche und induktive Widerstände). Oder hat irgendwer bisher LOW-ESR Kondensatoren verwendet?

Der Kondensator am Eingang soll einfach nur Strom liefern, wenn Strom gebraucht wird, d.h. wenn die Induktivität geladen wird. Da das Netzteil der DBox aber eine sehr konstante Stromquelle ist gegenüber einem einfachen Netztransformator mit Gleichrichter und sogar schon mit ausreichender Kapazität bestückt ist, kann auf eine weitere große Kapazitäten zugunsten eines kleinen "Abklatschkondensators" verzichtet werden.

[bitsucker]

@eule:

Wie kann man ein Datenblatt aber auch sooo fehlinterpretieren....
Wäre in dem Datenblatt ein Diagramm Wirkungsgrad in Abhängigkeit vom Laststrom (nicht Spannung), hättest du den Müll nicht geschrieben.

Zunächst mal fände ich es schön, wenn wir hier einen gewissen Diskussionsstil pflegen könnten. Dazu gehört für mich u.A. dass man Beiträge anderer nicht als "Müll" bezeichnet, sondern sachlich bleibt wenn man anderer Meinung ist.

Damit sich jeder selbst ein Bild von den Zusammenhängen machen kann, habe ich besagtes Diagramm mal eingefügt:



Der geneigte Leser sieht dort zwei Kurvenpaare, eines für eine Ausgangsspannung von 15V (die beiden oberen), eines für 5V (die beiden unteren). Für unseren Fall zutreffend sind die 5V Kurven, denn die 2,5" IDE Platten laufen nicht mit 15V (jedenfalls nicht lange ).

Daraus sieht man schon mal, dass man bei 5V nicht über 80% kommt. Weiterhin sieht man, dass die Kurve, die für 3A Laststrom gilt, weitgehend deutlich über der Kurve für 200mA Laststrom liegt. Dies gilt zumindest für Eingangsspannungen über 20V und diesen Fall haben wir ja bei der dbox.

Die Kurven gehen natürlich von den Standardbauteilen aus und sicher lässt sich da noch was optimieren und das ein oder andere Prozent mehr herausholen. Mir geht es aber hier um die Größenordnungen und die sieht man hier recht gut.

Schade, dass in der Applikationsschrift nicht ein ähnliches Diagramm wie Dieses enthalten ist:

Das liegt vermutlich daran, das "unser" Schaltregler ein Step-Down Regler ist (oder zumindest hier als solcher eingesetzt wird), also ein Regler, der aus einer höheren Eingangsspannung eine niedrigere Ausgangsspannung macht, während das von Dir verlinkte Diagramm für einen Step-UP Regler gilt (und noch dazu für einen komplett anderen Reglerbaustein), also einen, der aus einer niedrigen Eingangsspannung eine höhere macht.
Es gibt eine Unmenge an verschiedenen Schaltreglertypen und einen noch grössere Anzahl an unterschiedlichen Beschaltungen, die sich auch entsprechend unterschiedlich verhalten. Wenn wir hier also Vergleiche anstellen, sollten wir sinnvollerweise auch bei der selben "Obstsorte" bleiben.

Wenn du schon die Applikationsschrift zitierst, warum erwähnst du nicht, dass auch 100µF nicht ausreichen?

Weil ich im Applikationsteil keinen Hinweis darauf gefunden habe, dass die dort empfohlene Standardbeschaltung in der Praxis gar nicht nicht funktioniert.
Ein solcher Hinweis würde mich auch sehr wundern, denn solche Application Notes sind ja gerade dafür da, dem Entwickler zu zeigen, wie er es machen sollte.

Um Störstrahlung vom Eingang des Schaltkreises zu unterdrücken ist ein 100nF Kondensator weit besser geeignet als ein 100µF Elko

Das gilt für die Standardentkopplungskondensatoren über die man üblicherweise die Spannungsversorgung von Digital-ICs führt. Hier sind die Spitzenbelastungen durch schnelle Schaltvorgänge auch meist recht hochfrequent, da wäre ein Elko tatsächlich ungeeignet. Da geht es aber auch in der Regel um wesentlich geringere bzw "kürzere" Ströme als bei einem Schaltregler. Ein 100nF ist als Eingangskondensator eines Schaltreglers aber niemals ausreichend, noch nicht einmal bei einem 6-Phasen-Regler mit Schaltfrequenzen im MHz Bereich.

mit seinen langen Anschlußdrähten und dicken Wicklungen (ohmsche und induktive Widerstände). Oder hat irgendwer bisher LOW-ESR Kondensatoren verwendet?

Dass man bei Schaltreglern nur Kondensatoren einsetzt, die einen entsprechend geringen ESR haben, setze ich als selbstverständlich voraus (steht üblicherweise auch in den Application Notes).
Ich habe auch kein Wort davon gesagt, dass man unbedingt Elkos einsetzen sollte. Im Allgemeinen verwende ich bei Schaltreglerdesigns entsprechende SMD Tantalkondensatoren (das vereinfacht als Nebeneffekt auch die Bestückung, denn so ein bedrahtetes Bauteil bedeutet immer Handarbeit)

Code: Alles auswählen

Für die Nichtelektroniker:
Der Ersatz-Serien-Widerstand (ESR) bei einem Kondensator ist ein Mass dafür, wie hoch die Verluste im Inneren des Kondensators sind, die entstehen, wenn man dem Kondensator Strom entnimmt. Je höher der ESR desto grösser die Verluste. Diese Verluste werden in Wärme umgesetzt, was die Lebensdauer des Kondensators herabsetzt. Das gilt besonders für Elektrolytkondensatoren (erkennbar am Becherförmigen Gehäuse). Bei PC-Mainboards kann man diesen Effekt gelegentlich sehen: Die Kondensatoren blähen sich immer mehr auf (teilweise tritt auch Elektrolytflüssigkeit aus), verlieren ihre Kapazität und früher oder später läuft der Rechner nicht mehr hoch. Ursache ist meistens "Geiz ist geil", denn die Low-ESR Kondensatoren sind teurer als die herkömmlichen.

Der Kondensator am Eingang soll einfach nur Strom liefern, wenn Strom gebraucht wird, d.h. wenn die Induktivität geladen wird. Da das Netzteil der DBox aber eine sehr konstante Stromquelle ist gegenüber einem einfachen Netztransformator mit Gleichrichter und sogar schon mit ausreichender Kapazität bestückt ist, kann auf eine weitere große Kapazitäten zugunsten eines kleinen "Abklatschkondensators" verzichtet werden.

Wie ich schon sagte geht es ja auch gar nicht um die Stabilität des Netzteils der dbox, sondern es geht darum, wie lange die Zuleitung zwischen Quelle und Schaltregler ist. Könnte man das IDE Interface direkt neben dem Kondensator montieren, an dem die Spannung abgegriffen wird, bräuchte man tatsächlich keinen weiteren Kondensator.
In dem Fall wäre die Leitung zwischen Kondensator und Regler relativ kurz und damit die Störstrahlung gering.

Das Interface muss aber zwangsläufig an der vorgesehenen Stelle montiert werden und damit ist die Leitung zwischen dem Ladungslieferant im dbox Netzteil und dem Regler eben notwendigerweise sehr lang.

Es ist die LÄNGE der Leitung um die es hier geht und die ist auch die Ursache dafür, dass man eben am Reglereingang einen 100uF Kondesator vorsehen sollte.

[Charles Darwin jun.]

@Charles:
tut mir leid aber an der Stelle hörst Du dich jetzt an wie in einem Bedankomatenboard. Ich denke wenigstens das gute alte Tuxforum sollte Podium für ernsthafte und technische Diskussionen sein und bleiben. Für Sachen wie "Dankedankefürdiesestolleimageunddasnochtollereideinterfacedankeundnochmalskritiklosdanke" kann man andere Boards nutzen.

Servus,

...also mir jetzt Kritiklosigkeit zu unterstellen, is` ja heftig...
Solange...hier konstruktiv über Neuerungen diskutiert wird...ist es wunderbar...bitsucker scheint ja einiges drauf zu haben!

Ich sehe das IDE-IF nicht als Produkt dieses Forums...das war zu 90% die Leistung von DBoxBaer...
...manchmal werden Sachen hier nämlich solange kritisiert, bis keiner mehr Lust hat, was zu machen...

[eule]

Zunächst mal fände ich es schön, wenn wir hier einen gewissen Diskussionsstil pflegen könnten. Dazu gehört für mich u.A. dass man Beiträge anderer nicht als "Müll" bezeichnet, sondern sachlich bleibt wenn man anderer Meinung ist.

Das war aber noch sachlich.

Damit sich jeder selbst ein Bild von den Zusammenhängen machen kann, habe ich besagtes Diagramm mal eingefügt:



Der geneigte Leser sieht dort zwei Kurvenpaare, eines für eine Ausgangsspannung von 15V (die beiden oberen), eines für 5V (die beiden unteren). Für unseren Fall zutreffend sind die 5V Kurven, denn die 2,5" IDE Platten laufen nicht mit 15V (jedenfalls nicht lange )....

Wie dem aufmerksamen Leser auffallen sein wird, bietet keiner der für das IDE-Interface angebotenen Schaltregler 3A Ausgangsstrom an. Es bewegt sich alles im Rahmen von 0mA (Standby) bis max. 2A. Nun interessiert mich nicht der Wirkungsgrad von 3,3V, 5V oder 12V bei einem Strom von 3A sondern der Wirkungsgrad bei einer Ausgangsspannung von 5V und dem Ausgangsstrom von 0A bis 2A. Dazu hatte ich ein Beispieldiagramm gesucht und leider nicht gefunden.

Wenn wir hier also Vergleiche anstellen, sollten wir sinnvollerweise auch bei der selben "Obstsorte" bleiben.

Den Vergleich hast Du aber nun gemacht. Ich hab doch dazu geschrieben, dass:

Schade, dass in der Applikationsschrift nicht ein ähnliches Diagramm wie Dieses enthalten ist...

Also hab ich auf die Birnen hingewiesen um sie nicht zu dem Apfel zu tun...

Wenn du schon die Applikationsschrift zitierst, warum erwähnst du nicht, dass auch 100µF nicht ausreichen?

Weil ich im Applikationsteil keinen Hinweis darauf gefunden habe, dass die dort empfohlene Standardbeschaltung in der Praxis gar nicht nicht funktioniert.
Ein solcher Hinweis würde mich auch sehr wundern, denn solche Application Notes sind ja gerade dafür da, dem Entwickler zu zeigen, wie er es machen sollte.

Upps... In der von Dir zitierten Applikation Note (National Semiconductor) ist nicht nur ein Beispiel enthalten, es sind auch alle Berechnungen und Tabellen zu den Bauteilen, auch zum Eingangskondensator enthalten.

...Da geht es aber auch in der Regel um wesentlich geringere bzw "kürzere" Ströme als bei einem Schaltregler. Ein 100nF ist als Eingangskondensator eines Schaltreglers aber niemals ausreichend, noch nicht einmal bei einem 6-Phasen-Regler mit Schaltfrequenzen im MHz Bereich.

Erstens schmeißt du jetzt Tomaten in den Whiskey.

Zweitens ist der 100nF kein Eingangskondensator, er soll nur die Transienten mildern, die beim Ein- und Ausschalten des Ladestromes der Drossel auftreten. Ich weiss nicht, ob du schon mal von der Fourrier-Transformation gehört hast, wenn ja, dann weisst du auch, was Transienten sind bzw. in welchem Frequenzbereich sich das abspielt.

Drittens ist die Eingangsspannung für den Schaltregler keine ungeregelte, pulsierende Spannung, sondern eine durch einen Schaltregler aufbereitete sehr gut stabilisierte Spannungsquelle, die mit ausreichenden Kapazitäten ausgelegt ist, damit die Eingangsspannung an unserem Schaltregler nie unter die Mindestspannung fällt. Da dieses bei einem ungeregelten Netzteil nicht garantiert ist, muss jemand dafür sorgen, dass bei zu geringer Eingangsspannung (damit auch kaum Strom) auch genügend Strom zur Verfügung steht, um die Drossel zu "laden". Das ist die Aufgabe des Elko's.

...sondern es geht darum, wie lange die Zuleitung zwischen Quelle und Schaltregler ist. Könnte man das IDE Interface direkt neben dem Kondensator montieren, an dem die Spannung abgegriffen wird, bräuchte man tatsächlich keinen weiteren Kondensator.
In dem Fall wäre die Leitung zwischen Kondensator und Regler relativ kurz und damit die Störstrahlung gering.

siehe oben... Der Elko beseitigt keine Störungen, er liefert den Ladestrom, wenn das "Netzteil" dazu nicht in der Lage ist. Die "Störungen" werden zuverlässig durch den 100nF Kondensator beseitigt.

Es ist die LÄNGE der Leitung um die es hier geht und die ist auch die Ursache dafür, dass man eben am Reglereingang einen 100uF Kondesator vorsehen sollte.

Oben stand noch, dass damit die Störungen beseitigt werden sollen, nun ist es die Leitungslänge. Dann hängt also deiner Meinung nach die Höhe der Kapazität von der Leitungslänge ab?

Die Eingangskapazität wird nur aus dem Ausgangsstrom und der Eingangsspannung bestimmt. Nicht aus der Leitungslänge und auch nicht aus der Frequenz oder Induktivität der Drossel. Warum wohl?

Lass dir das mal von jemandem erklären, der auch mit Umsetzern arbeitet und nicht von einem Berufsschullehrer...

[eule]

Bitte um Verzeihung für die Doublette....

[eule]

Was für ein Schaltregler?

Ich versuche mal mit folgendem Zitat bei Dir die Eiweißablagerungen an den Synapsen zu lösen:

Original von Friedel
Ich habe keinen Bock mehr auf Diskussionen und cancle hiermit das Netzteil. Soll es bauen wer will. Von mir jedenfalls kommt keins.

Na, dämmerts?

[bitsucker]

Zitat aus dem National Datenblatt :

Code: Alles auswählen

4. Input Capacitor (CIN ) An aluminum or tantalum
electrolytic bypass capacitor located close to the
regulator is needed for stable operation.
4. Input Capacitor (CIN ) A 100 µF, 25V aluminum
electrolytic capacitor located near the input and ground
pins provides sufficient bypassing.

100nF und 100 uF liegen, wie schon gesagt, um den Faktor Tausend auseinander und mehrere cm Kabel kann man beim besten Willen nicht mehr als "close to" bezeichnen.

Ich weiss nicht, ob du schon mal von der Fourrier-Transformation gehört hast

Ja, habe ich. Das ist Bestandteil eines E-Technik Studiums. Ich glaube aber nicht, dass Diskussionen über das Spektrum von Transienten hier besonderes Interesse finden würden.

und nicht von einem Berufsschullehrer...

Mit einem solchen hatte ich noch nichts zu tun.

Drittens ist die Eingangsspannung für den Schaltregler keine ungeregelte, pulsierende Spannung, sondern eine durch einen Schaltregler aufbereitete sehr gut stabilisierte Spannungsquelle, die mit ausreichenden Kapazitäten ausgelegt ist, damit die Eingangsspannung an unserem Schaltregler nie unter die Mindestspannung fällt.

Das bestreite ich doch auch gar nicht. Bei genauerem Lesen meiner Beiträge müsste auffallen, dass ich von einem pulsierenden STROM gesprochen habe, nicht von einer pulsierenden Spannung.
Das Netzteil der dbox kann so stabil und sauber sein wie es mag, das ändert nichts daran, dass der IDE Schaltregler diesem keinen kontinuierlichen, sondern einen pulsierenden STROM entnimmt. Und dieser sorgt bei entsprechender Leitungslänge (= Antenne) eben für Störstrahlung. Damit sind nicht irgendwelche Störungen gemeint. die der Regler evtl. auf die Eingangsspannung einkoppelt, sondern welche, die die Leitung in Form elektromagnetischer Wellen verlassen.

Oben stand noch, dass damit die Störungen beseitigt werden sollen, nun ist es die Leitungslänge. Dann hängt also deiner Meinung nach die Höhe der Kapazität von der Leitungslänge ab?

Nein, bitte auch hier nochmal lesen. Die Leitungslänge zwischen dem Eingangskondensator und dem Regler hat etwas mit der Intensität der Abstrahlung zu tun.
Die Störungen werden durch die Reglernahe Platzierung des Kondensators nicht beseitigt, sondern sie entstehen erst gar nicht, weil das kurze Leitungsstück eben nicht so stark strahlt.


Dass der Eingangskondensator eine Schaltreglers möglichst nahe am Reglereingang zu platzieren ist und dass ein Wert von 100nF nicht ausreichend ist, sind absolute Basics des Schaltreglerdesigns, die Dir auch jeder Hardwareentwickler bestätigen wird, der solche Designs schon gemacht hat.

Hier noch ein Beispiel aus der Praxis:
Wir hatten mal bei einer Nullserie eines Rechnerboards für einen Fahrkartenautomaten den Effekt, dass alle 10 Boards fehlerhaft arbeiteten, während die Prototypen einwandfrei funktionierten. Alle Boards zeigten den gleichen Fehler.
Nach einiger Suche stellte sich heraus, dass ein eigentlich statisches Signal, dass zu Konfigurationszwecken standardmäßig durch einen Jumper auf Masse gelegt war, so starke Spikes aufwies, dass der daran angeschlossene Eingang eines Baustein ständig schaltete.

Nach weiterer Suche stellte sich heraus, dass die 4 Eingangskondensatoren des Schaltnetzteils (4 * 100uF) mit falschen Bauteilen bestückt worden waren (Es wurden Typen mit 6,3V Spannungsfestigkeit statt 35V Typen bestückt). Bei 24V Eingangsspannung (aus einem Industrietauglichen Netzteil) waren diese daher hoffnungslos überlastet und weitgehend wirkungslos. Den Strom lieferte nun ein hinter der Spannungsversorgungsbuchse sitzender Elko. Von dort führte die Leitung über ein Connectorboard ca. 20 cm zu einer Federleiste über die das Rechnerboard mit dem Connectorboard verbunden war. Kurz hinter der Messerleiste des Rechnerboards befand sich dann das Schaltnetzteil.

Die Strecke zwischen Elko und Reglereingang hat hier also so eine gute Sendeantenne abgegeben, dass man damit auf einer etliche cm entfernten und relativ kurzen Leitung die sozusagen nach Masse kurzgeschlossen war, noch High Impulse im Takt der Schaltreglerfrequenz messen konnte.
(Ja, das waren wirklich elektromagnetische Einkoppelungen, die Spannung am Ausgang des Schaltnetzteils war, trotz der überlasteten Eingangskondensatoren, sauber) Eine ähnliche Konstellation hat man bei dem IDE Schaltregler in der Box (ungenügender Eingangskondensator und lange Leitung zur Spannungsversorgung), wobei bei unserem Design allerdings die Schaltfrequenz auch deutlich höher war als 52kHz.

Ich werde das Thema damit für meinen Teil erstmal abschließen. Mir genügt es, wenn meine Designs vernünftig funktionieren und beim EMV-Test nicht durchfallen. Darüber wer hier im Forum nun wessen Ausführungen glaubt oder nicht, bin ich relativ leidenschaftslos und Käppi hat ja schon angekündigt, dass er das mit dem Kondensator ändern will, damit ist der Sache ja dann schon geholfen.

Ich denke auch, dass wir hier mittlerweile etwas off-topic sind und die Mehrheit unter dem Thema dieses Threads vermutlich etwas anderes erwartet als Diskussionen über nachlesbare Grundlagen.

[Charles Darwin jun.]

Naja...das sah mir jetzt verdammt nach "ich weiss mehr als du" Diskussion aus...

...ich bin ganz auf deiner Seite bitsucker...deine Ausführungen haben mich als Laien überzeugt...außerdem mag ich Eule`s Schreibstil net

...aber das hilft dir auch net wirklich weiter

[eule]

Ich denke auch, dass wir hier mittlerweile etwas off-topic sind und die Mehrheit unter dem Thema dieses Threads vermutlich etwas anderes erwartet als Diskussionen über nachlesbare Grundlagen.

Dann machen wir das einfacher:

Du hast Recht und ich hab meine Ruhe....

[bitsucker]

Naja...das sah mir jetzt verdammt nach "ich weiss mehr als du" Diskussion aus...

Ja, den Eindruck habe ich inzwischen auch.

Das Grundproblem ist wohl, dass eule und Ich von zwei ganz verschiedenen Effekten sprechen, was aber anscheinend erst einer von uns gemerkt hat

Die Transienten, die eule anspricht entstehen zwangsläufig beim Betrieb (vor allem "schneller") digitaler Bausteine. Durch einen Kondensator am Spannungsversorgungsanschluss des Bausteins verhindert man, dass diese auf die Spannungsversorgung übergehen und damit andere Bauteile stören können. 100nF sind da ein Standardwert, der meistens hilft.
Also hier volle Übereinstimmung.

Wovon ich spreche, sind aber keine elektrischen sondern elektromagnetische Störungen, die durch das Fliessen eines pulsierenden STROMs zwischen Spannungsquelle und Schaltregler entstehen können.
Die filtert man nicht, sondern man verhindert so weit wie möglich, dass sie überhaupt erst entstehen. Dazu braucht man den nahe am Regler befindlichen Eingangskondensator (kurze Leitung - kurze Antenne) und der muss eben eine entsprechend hohe Kapazität haben um den Stromfluss (nicht die Spannung) "glätten" zu können.

Es wäre toll wenn dafür 100nF ausreichend wären, das würde bei der Hardwareentwicklung viel Platz (auf den Boards) und Geld sparen, aber das ist halt (auch bei unendlicher Fortsetzung dieses Threads) leider nicht der Fall.

[Tommy]

Also ich für meinen Teil fand/finde alle Ausführungen in diesem Thread sehr interessant und habe gerne mitgelesen (und viel gelernt). Wenn solche Diskussionen hier im Tuxboard Standard wären könnte man ZUSAMMEN richtig was auf die Beine stellen. Leider findet man solche Threads nicht oft, da es den meisten Leuten nur darum geht irgendwas freizubekommen und deshalb die Anfängesektion zuballern.

[eule]

Die Transienten, die eule anspricht entstehen zwangsläufig beim Betrieb (vor allem "schneller") digitaler Bausteine. Durch einen Kondensator am Spannungsversorgungsanschluss des Bausteins verhindert man, dass diese auf die Spannungsversorgung übergehen und damit andere Bauteile stören können. 100nF sind da ein Standardwert, der meistens hilft.
Also hier volle Übereinstimmung.

Wovon ich spreche, sind aber keine elektrischen sondern elektromagnetische Störungen, die durch das Fliessen eines pulsierenden STROMs zwischen Spannungsquelle und Schaltregler entstehen können.
Die filtert man nicht, sondern man verhindert so weit wie möglich, dass sie überhaupt erst entstehen. Dazu braucht man den nahe am Regler befindlichen Eingangskondensator (kurze Leitung - kurze Antenne) und der muss eben eine entsprechend hohe Kapazität haben um den Stromfluss (nicht die Spannung) "glätten" zu können.

Bist du dir da sicher? Ich zitiere mal wieder aus der Applikationsschrift:

INPUT CAPACITOR
CIN — A low ESR aluminum or tantalum bypass capacitor is needed between the input pin and ground pin. It must be located near the regulator using short leads. This capacitor prevents large voltage transients from appearing at the input, and provides the instantaneous current needed each time the switch turns on. The important parameters for the Input capacitor are the voltage rating and the RMS current rating. Because of the relatively high RMS currents flowing in a buck regulator’s input capacitor, this capacitor should be chosen for its RMS current rating rather than its capacitance or voltage ratings, although the capacitance value and voltage rating are di-rectly related to the RMS current rating.

edit
etwas sachlicher
/edit

Da steht, dass der Eingangskondensator große Spannungstransienten verhindern soll, die am Eingang auftauchen. Gleichzeitig liefert dieser Kondensator den Strom der beim Einschalten (des Schalttransistors zum laden der Drossel) sofort benötigt wird. Hochfrequente (Spannungs-) Transienten kann man ja sehr gut mit einem 100nF Kondensator blocken (da stimmen wir überein...).

Mir ist auch klar, dass da über den Draht ein ziemlich großer Strom pulsartig fließt. Nur glättet man den nicht nur mit einem Kondensator sondern mit einem Tiefpass (Drossel + Kondensator).

Warum der Fokus auf einen einzelnen Draht, wenn der große elektromagnetische Strahler doch immer noch die Stabferritdrossel auf gorcon's Schaltwandler ist? Dagegen sind doch die Abstrahlungen auf den Spannungsführenden Drähten vernachlässigbar klein. Ok, auf dem IDE2-Interface wird ein Ringkern eingesetzt....

[Z80]

Lass dir das mal von jemandem erklären, der auch mit Umsetzern arbeitet und nicht von einem Berufsschullehrer...

völlig daneben sowas...
@bitsucker: danke für die auffrischung der "basics".

[Z80]

Also ich für meinen Teil fand/finde alle Ausführungen in diesem Thread sehr interessant und habe gerne mitgelesen (und viel gelernt). Wenn solche Diskussionen hier im Tuxboard Standard wären könnte man ZUSAMMEN richtig was auf die Beine stellen. Leider findet man solche Threads nicht oft, da es den meisten Leuten nur darum geht irgendwas freizubekommen und deshalb die Anfängesektion zuballern.

jepp, leider viel zu viel dummschwatz und/oder zu viel profilneurosen, statt wie hier von bitsucker angestoßen harte fakten in sachlicher diskussion zu erörtern.

[eule]

Lass dir das mal von jemandem erklären, der auch mit Umsetzern arbeitet und nicht von einem Berufsschullehrer...

völlig daneben sowas...

Bist du etwa einer? Ich habe leider die Erfahrung machen müssen, dass Leute dieser Berufsgruppe einfach zu lange aus der Praxis heraus sind. Dadurch können sie über aktuelle Entwicklungen nicht mehr berichten und stellen oftmals Dinge falsch dar.

In meinem Fall wurde behauptet, dass die Eigenschaften von Stoffen von den enthaltenen Atomen bestimmt werden...

[Z80]

Lass dir das mal von jemandem erklären, der auch mit Umsetzern arbeitet und nicht von einem Berufsschullehrer...

völlig daneben sowas...

Bist du etwa einer? Ich habe leider die Erfahrung machen müssen, dass Leute dieser Berufsgruppe einfach zu lange aus der Praxis heraus sind. Dadurch können sie über aktuelle Entwicklungen nicht mehr berichten und stellen oftmals Dinge falsch dar.

In meinem Fall wurde behauptet, dass die Eigenschaften von Stoffen von den enthaltenen Atomen bestimmt werden...

Deine fachlichen Kompetenzen kann ich schlecht beurteilen, mit Deinen "Soft-Skills" scheints aber nicht soweit her zu sein...
Unter sachlicher Diskussion verstehe ich jedenfalls etwas anderes. Aber das ist hier im Forum ja leider Gewohnheit.
Und nein ich bin kein Berufsschullehrer, bilde mir aber ein als Dipl.-Ing. ET schon mitreden zu können, wenn ich auch sicherlich kein Spezialist im Bereich Leistungselektronik bin.
Bei Deinen hier getätigten Aussagen ggü. dieser Berufsgruppe, läßt sich jedoch eine gewisse Überheblichkeit nicht überhören - aber das vergeht (Stichwörter: Lebenserfahrung, unerlaubte Verallgemeinerung).

Und das bitsucker dieser Berufsgruppe entspringt glaubst Du doch auch nicht wirklich, oder? Also worum gehts hier eigentlich?

Wie auch immer, macht Ihr hier mal weiter.

[eule]

Also worum gehts hier eigentlich?

Ich bring es mal auf den Punkt:
Wie hoch ist der Wirkungsgrad des Schaltwandlers im "Normalbetrieb" in der DBox?

Lt. bitsucker soll der Wirkungsgrad des Schaltwandlers bei einer Ausgangslast am Höchsten sein, daher soll er für diesen Schaltwandler (bei 5V Ausgangsspannung) niemals über 80% steigen können. Begründet wurde dies mit dem Vorhandensein eines Diagramms in der Application Note.

Diese These habe ich als Müll bezeichnet. Ich korregiere mich auch gerne und behaupte, dass diese Aussage nicht korrekt ist. Der höchste Wirkungsgrad befindet sich im Bereich von 0,1A bis 0,5A Ausgangslast, da die ohmschen Verluste bei größeren Strömen den Wirkungsgrad fallen lassen und bei kleineren Strömen der Eigenverbrauch des Schaltkreises den Wirkungsgrad bestimmt. Aber hier wiederhole ich mich...

Ich werde in zwei Wochen mal eine Meßreihe durchführen und Diagramm selber erstellen, da ich im Internet immer noch nichts passendes gefunden habe. Dann kann mir niemand anhängen, dass das Diagramm nicht zum ausgewählten Schaltkreis bzw. zum Schaltwandlertyp passt.

[bitsucker]

Der höchste Wirkungsgrad befindet sich im Bereich von 0,1A bis 0,5A Ausgangslast, da die ohmschen Verluste bei größeren Strömen den Wirkungsgrad fallen lassen und bei kleineren Strömen der Eigenverbrauch des Schaltkreises den Wirkungsgrad bestimmt. Aber hier wiederhole ich mich...

Ja, davon wird es aber auch nicht richtiger

Lass uns doch noch mal auf das Diagramm schauen:



Wir sind uns doch bestimmt darüber einig, dass wir von 5V Ausgangsspannung ausgehen und dass unsere Eingangsspannung bei mindestens 27V liegt. Also sind hier die beiden unteren Kurven interessant. Edit: genauer gesagt, die rechte Hälfte der beiden unteren Kurven
Der Beschriftung der Kurven nach, gehört die obere Kurve zu einem Laststrom von 3A und die untere zu einer Last von 200mA.
Bisher Einwände?

Wenn ich nun etwa bei 27V auf der X-Achse nach oben gehe, sehe ich dort bei der 200mA-Kurve einen Schnittpunkt von etwa 77% Wirkungsgrad und bei der 3A-Kurve etwa 80%. Daraus schliesse ich, dass der Wirkungsgrad hier bei 3A Last höher ist als bei 200mA, denn 80 > 77.

Nun fehlen hier leider Kurven für irgendwelche Zwischenwerte wie 0,5A oder 2A, aber ich denke wir können davon ausgehen, dass diese irgendwo zwischen den beiden "Extremkurven" liegen werden.

Der Wirkungsgrad nimmt bei dieser Reglerschaltung also leicht zu, wenn der Laststrom steigt.

Dass die Ohm'schen Verluste bei höherem Laststrom notwendigerweise zunehmen ist schon richtig, aber das Thema Verluste muss man sich hier etwas genauer anschauen:

Wir haben hier ja zwei verschiedene Strompfade:

Während der Einschaltphase des Reglers fliesst der Strom durch den im Regler integrierten FET zur Spule und erzeugt im FET Ohm'sche Verluste.

Während der Ausschaltphase fliesst der Strom durch die Freilaufdiode und es entstehen nun in dieser Ohm'sche Verluste.

Nun ist es aber so, dass die üblicherweise in Schaltreglern verwendeten FETs heutzutage einen so geringen Einschaltwiderstand haben, dass die dort entstehenden Verluste deutlich kleiner sind als die, die in den Freilaufdioden entstehen.
Wenn nun aber der Laststrom zunimmt, ändert der Regler ja das Tastverhältnis. Die Einschaltphase wird gegenüber der Ausschaltphase länger. Die höheren Verluste der Diode wirken sich nun weniger stark aus (weil sie am Gesamtstrom weniger stark beteiligt ist) und so nimmt der Wirkungsgrad eben etwas zu.

Die vergleichsweise grossen Verluste der Dioden sind ja auch der Grund warum es Synchronregler gibt, die einen zweiten FET besitzen (oder einen externen steuern können), der während der Ausschaltphase die Funktion der Diode übernimmt.

Auf Deine Messungen bin ich aber in jedem Fall gespannt, denn Papier (Datenblätter) ist ja bekanntlich geduldig.

Code: Alles auswählen

Anmerkung für Nicht-elektroniker:

FET = Feldeffekttransistor. Das ist der "Schalter" im Schaltregler.

[eule]

Erst einmal meine Hochachtung für die wirklich sehr ausführlichen Erklärungen.

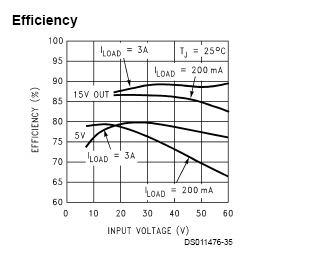
Wir sind uns doch bestimmt darüber einig, dass wir von 5V Ausgangsspannung ausgehen und dass unsere Eingangsspannung bei mindestens 27V liegt. Also sind hier die beiden unteren Kurven interessant. Edit: genauer gesagt, die rechte Hälfte der beiden unteren Kurven
Der Beschriftung der Kurven nach, gehört die obere Kurve zu einem Laststrom von 3A und die untere zu einer Last von 200mA.
Bisher Einwände?

Nein, Aber ich habe Ergänzungen.

Wir betrachten hier also einen Schltregler, der für einen Ausgangsstrom von 3A ausgelegt ist. Damit wird der Schaltregler in der nichtlückenden (continuous mode) Betriebsart eingesetzt. Der lückende Betriebsmode würde nur bei Strömen unter 1,0A in Frage kommen [1][2]. Weiteres dazu später...

Nun fehlen hier leider Kurven für irgendwelche Zwischenwerte wie 0,5A oder 2A, aber ich denke wir können davon ausgehen, dass diese irgendwo zwischen den beiden "Extremkurven" liegen werden.

Der Wirkungsgrad nimmt bei dieser Reglerschaltung also leicht zu, wenn der Laststrom steigt.

Das Irgendwo heißt, dass du auch nicht weißt, was dazwischen liegt, aber du gehst davon aus, dass der Wirkungsgrad (((linear))) steigen muss, wenn der Ausgangsstrom steigt? Wenn der Ausgangsstrom steigt, müssen also die Verluste sinken?

Dass die Ohm'schen Verluste bei höherem Laststrom notwendigerweise zunehmen ist schon richtig, aber das Thema Verluste muss man sich hier etwas genauer anschauen:
Während der Einschaltphase des Reglers fliesst der Strom durch den im Regler integrierten FET zur Spule und erzeugt im FET Ohm'sche Verluste.
Während der Ausschaltphase fliesst der Strom durch die Freilaufdiode und es entstehen nun in dieser Ohm'sche Verluste.

Genau. Auch hier stimmen wir überein.

Wenn nun aber der Laststrom zunimmt, ändert der Regler ja das Tastverhältnis. Die Einschaltphase wird gegenüber der Ausschaltphase länger....

Aber hier hast du einen Irrweg beschritten. Nicht der Strom bestimmt das Tastverhältnis, es wird von der Spannung bestimmt.

Die Herleitung mag zwar nun für viele langweilig sein, es gibt aber auch einige User, die das Thema interessiert:

Bei einem "Step-Down-Converter" wird eine Spannung von einem hohen auf auf ein niedrigeres Niveau gesenkt. Da die Leistung gleich bleibt, wird ein kleiner Eingangsstrom in einen größeren Ausgangsstrom umgesetzt:

Pe = Pa
Ue * Ie = Ua * Ia

oder

Ua / Ue = Ie / Ia

Das ist nichts anderes, was auch ein normaler Wechselstromtransformator macht. Nun aber zum Tastverhältnis [1]:

Die Speicherdrossel wird wärend der Einschaltphase Te mit Energie vollgepumpt. Diese Energie hängt auch ab von der Spannung, die an der Drossel anliegt. Um die Herleitung zu vereinfachen, vernachlässige ich alle Verluste, die Auftreten können: Innenwiderstände von FET's und Spannungsabfälle an Dioden. Damit liegt an der einen Seite der Drossel die Spannung Ue auf der anderen Seite die Spannung Ua an. Die Differenz entspricht der Spannung an der Drossel Udr = Ue - Ua. Damit ergibt sich für die reingesteckte Energie:
Ee = Te * Udr = Te * (Ue-Ua)

Auf der Ausgangsseite ist das einfacher. Die Energie die der Drossel entnommen werden kann wird von der Ausschaltphase Ta und der Drosselspannung bestimmt:
Ea = Ta * Udr = Ta * Ua

Da die reingesteckte Energie gleich der Energie sein soll, die wir (unter Vernachlässigung aller Verluste) auch am Ausgang erwarten, ergibt sich:
Ee = Ea

Te * (Ue-Ua) = Ta * Ua

Das lösen wir mal nach Ua auf:

Ua * Ta = Te * Ue - Te * Ua

Ua * Ta + Te * Ua = Te * Ue

Ua (Ta + Te) = Te * Ue

Ua = Ue * Te / (Ta +Te)

Damit erkennt man, dass mit dem Tastverhältnis die Spannung am Ausgang eingestellt wird. Ein Tastverhältnis von 1:1, d.h. Te = Ta ergibt am Ausgang die Hälfte der Eingangsspannung. Diese Herleitung gilt aber nur für den nichtlückenden Betrieb und damit für den hier verwendeten Schaltregler. Jetzt noch der Beweis, dass eine Stromänderung das Tastverhältnis nicht ändern kann:

Ua = Ue * Te / (Ta +Te)

ein klein wenig umgestellt:

Ua / Ue = Te / (Ta +Te)

Weiter oben haben wir aber schon folgende Formel hergeleitet:

Ua / Ue = Ie / Ia

damit ergibt sich wiederum:

Ua / Ue = Ie / Ia = Te / (Ta +Te)

Daraus erkennt man: würde sich durch einen höheren Stromfluß am Ausgang das Tastverhältnis ändern, würde sich automatisch auch die Ausgangsspannung verändern (bei konstanter Eingangsspannung von 27V). Diese soll aber konstant 5V betragen...

Dass die Spannungsreglung beim LM2596 über das Tastverhältnis vorgenommen wird, kann man sich auch aus der Applikationsschrift [2] herleiten: Auf Seite 4 gibt es den Parameter min/max duty cycle mit den Fußnoten 8 und 9.

Ich fange mal mit Fußnote 9 an: Wird der Meßeingang des Schaltkreises vom Rest der Schaltung isoliert und auf Masse gelegt, wird der Ausgangstransistor dauerhaft eingeschaltet (Te = 100%). Damit steht die volle Eingangsspannung am Ausgang an. Dieses kann auch in die Formel für das Tastverhältnis eingesetzt werden:

Ua = Ue * Te / (Ta +Te)

Ua = 27V * 100 / (0 + 100)

Ua = 27V * 100 / 100 = 27V

Gleiches gilt für Fußnote 8: Wird der Meßeingang des Schaltkreises vom Rest der Schaltung isoliert und auf den vorgegebenen Spannungswert gelegt, wird der Ausgangstransistor dauerhaft ausgeschaltet (Te = 0%). Damit ist die Ausgangsspannung 0V.

Ua = Ue * Te / (Ta +Te)

Ua = 27V * 0 / (100 + 0)

Ua = 27V * 0 = 0V

Durch diese Probe wäre die Gültigkeit meiner Berechnungen für den LM2596 belegt.

Die höheren Verluste der Diode wirken sich nun weniger stark aus (weil sie am Gesamtstrom weniger stark beteiligt ist) und so nimmt der Wirkungsgrad eben etwas zu.

Aus der vorher gewonnenen Erkenntnis können die Verluste nicht geringer werden, da sich das Tastverhältnis nicht ändert. Im Gegenteil, die Verluste werden größer:

Damit jeder im Kopf folgen kann, nehme ich mal an, dass die Eingangsspannung 25V und die Ausgangsspannung 5V beträgt. Damit ergibt sich ein Tastverhältnis von 20 (Te) zu 80 (Ta).

Nun werfen wir einen Blick in das Datenblatt der Diode [3]: bei 3A Durchlasspannung fallen an dieser Diode ca. 0,3 V ab. Die Verlustleistung berechnet sich wie folgt:

P = U * I
P = 0,3V * 3A
P = 0,9W

Da bei einem Tastverhältnis von 20 zu 80 die Diode nur zu 80% mit den 3 A belastet wird:

Pv = 0,9W *0,8
Pv = 0,72W

Verhältnis Verlustleistung zu Ausgangsleistung:
x = Pv / Pa
x = 0,72W /15W <- =3A * 5V
x= 0,048 = 4,8%

Nun rechnen wir das Ganze mal für einen Ausgangsstrom von 200mA aus (Uf ~0,2V bei 0,2A):

Pv = 0,2V *0,2A *0,8
Pv = 0,04W *0,8
Pv = 0,032W

Verhältnis Verlustleistung zu Ausgangsleistung:
x = Pv / Pa
x = 0,032W /1W <- =0,2A * 5V
x= 0,032 = 3,2%

Edit:
Nachdem ich noch ein paar Zwischenwerte berechnet habe eine kleine Korrektur:

Zwischenwerte:
0,6A -> 0,12W -> 4%
1,0A -> 0,27W -> 4,3%
2,0A -> 0,6 W -> 4,8%

Wie anhand dieser Berechnungen zu sehen ist, steigen die Verluste parabelförmig [statt linear /edit] mit dem Ausgangsstrom an. Sie werden aber nicht geringer. Ähnlich verhält es sich mit dem FET. Dieser hat laut Datenblatt eine Sättigungsspannung von 1,16V bei 3A und ca. 0,8V bei 200mA. Auch hier steigen die Verluste mit dem Strom an. Nun wird auch meine (rhetorische) Frage vom Anfang des Textes beantwortet, dass bei steigendem Ausgangsstrom auch die Verluste steigen müssen.

Weshalb ist trotz nachgewiesen geringeren Verlusten der Wirkungsgrad bei 0,2A kleiner als bei 3A? Bisher wurde der Leistungsbedarf des Schaltreglers selbst in die Berechnungen nicht einbezogen. Dieser ist über den gesamten Regelbereich relativ konstant.

Bei kleinsten Strömen ist der Wirkungsgrad sehr schlecht, da der Schaltkreis mehr Leistung in Wärme umsetzt (Eigenverbrauch), als an Ausgangsleistung geliefert wird. Der optimale Wirkungsgrad müßte im Bereich von 0,1A bis 0,5A liegen, weil hier der Einfluß des Eigenverbrauchs deutlich abnimmt und noch nicht die ohm'schen Verluste wirken die bei hohen Strömen deutlich zunehmen.


Literaturverzeichnis:
[1] http://www.sprut.de/electronic/switch/schalt.html#down
[2] http://www.ortodoxism.ro/datasheets/nat ... 012583.PDF
oder http://www.acmesystems.it/download/LM2596.pdf
[3] http://www.ortodoxism.ro/datasheets/mic ... 823-25.pdf
oder http://www.datasheetarchive.com/pdf/116316.pdf